Autor: Matthias Krieger, See Club Zug
Wer den Rudersport liebt, und das werden die meisten sein die den Ruderspritzer lesen, hat sich sicher ab und zu Gedanken gemacht weshalb über gewisse Details der Rudertechnik jahrelang debattiert wird und sogar erfahrene RuderkollegInnen sich nicht immer einig sind wie wichtig gewisse Details eben doch sind. Es gibt viele sehr gute Bücher über den Rudersport, u.a. eine wissenschaftlich exzellente ETHZ Dissertation von Franz Gravenhorst [1] welche 2015 auf englisch publiziert worden ist. Sie enthält zahlreiche messtechnische Details und statistische Analysen von Spitzensportlern und ist wissenschaftlich sehr fundiert. Ebenso lehrreich und in vielen praktischen Aspekten noch viel umfangreicher und anschaulicher präsentiert ist die schöne Sport-Abiturarbeit von Sascha Adrian[2] vom Gymnasium Rüsselsheim aus dem Jahre 2004. Viel detaillierter auf die gesamte Biomechanik des Ruderns, dem Zusammenspiel von Ruderern und Boot und Strömung im Wasser geht das Lehrbuch von Ditmar Wick [3] zur Biomechanik sportlicher Bewegungen ein. Einige Argumente die ich hier skizziere werden dort viel detaillierter dargelegt. Ich bin selber Physiker und an vielen theoretischen Grundlagen interessiert die unser tägliches Leben beeinflussen. Meine Lieblingsgebiete der Physik sind heute zwar Halbleiterphysik, Elektrodynamik, Quantenmechanik und Gruppentheorie sowie mathematische Methoden der Physik, aber der Rudersport ist eine ebenso spannende wie amüsante Spielwiese für klassische Mechanik und Fluiddynamik.
In meinen regelmässigen Coaching Trainings als Götti für neue RuderInnen im Club habe ich festgestellt dass es mir leichter gefallen ist die Physik als Begründung herzuziehen für gewisse technische Forderungen die zu Beginn oft gestellt werden da sie nicht immer intuitiv sind und deshalb mit Disziplin eingeübt werden müssen. Deshalb bin ich am Ende des Göttitrainings von Maren angefragt worden ob ich auch mal einen Artikel zum Thema Physik des Rudersportes schreiben könne. Hier ist er!
In diesem Artikel erläutere ich einige physikalische Grundlagen zu diesen Themen:
- Gleichgewicht im leichten Rennboot (Beispiel Skiff)
- Kraftstoss als physikalisches Prinzip des muskelbetriebenen Bootsantriebs
- Dynamik und Optimierung der Vorrollbewegung
- Effizienz des Kraftstosses während des Ruderns
- Effizienz der Kraftübertragung auf die Ruderblätter anhand des Blattwinkels
- Synchronisierung der Kraftstösse in einem grösseren Ruderteam
Als Alternative zu den vielen Publikationen zum Rudersport die vor allem erklären WIE gerudert werden soll, beschreibe ich hier einige wichtige Effekte WARUM so gerudert werden muss, weil die Physik schlicht keine Alternative anbietet.
1 Physik der Gleichgewichtslage im leichten Rennboot
Zu Beginn möchte ich eine physikalische Grundlage des Gleichgewichts in leichten Rennbooten beschreiben, die vor allem im Skiff ausgeprägt anspruchsvoll zu meistern ist für AnfängerInnen des Rudersports. Hier muss ich etwas in die mathematische Trickkiste greifen um korrekt zu beschreiben was mit einem Skiff passiert wenn die Gleichgewichtslage nicht mehr ausbalanciert ist. Ein Skiff ist ein extrem leichtes Sportboot [4] mit ca 14 kg Masse, ist also im Durchschnitt mindestens Faktor 5 leichter als der Ruderer selbst, das ist die Hauptursache für Stabilitätsprobleme die AnfängerInnen oft antreffen. Die Physik hat leistungsfähige Methoden entwickelt beliebig komplexe Verteilungen von Skalarfeldern (physikalische Grösse charakterisiert durch eine einzige Zahl an jedem Ort im Raum) zu beschreiben die nicht gleichmässig im Raum verteilt sind. Ein Skalarfeld ist z.B. eine Massenverteilung oder eine elektrische Ladungsverteilung die ortsabhängig ist. Ein Ruderer oder eine Ruderin in einem Skiff stellt aus physikalischer Sicht eine ziemlich komplexe Massenverteilung dar die in allgemeinster Form in eine Multipolentwicklung zerlegt werden kann um die Kräfte zu analysieren die auf die Massenverteilung einwirken.
1.1 Allgemeine Beschreibung der Massenverteilung von Ruderer/in im Skiff
Jede beliebige Massendichteverteilung wird in der Physik charakterisiert durch ein Gravitationspotentialfeld das nach Multipolen entwickelt werden kann um die räumliche Anisotropie (Abweichung von der Kugelsymmetrie) exakt zu beschreiben und zu verstehen.

Formel (1)


Formel (2)

Die erste Formel (1) beschreibt die allgemeine Multipolentwicklung einer beliebig komplexen Massendichteverteilung nach orthogonalen sphärischen Kugelfunktionen wobei die zahlreichen Koeffizienten die allesamt gemäss Formel (2) berechnet werden müssen die sogenannten Multipolmomente der Massendichteverteilung bezeichnen. Diese Berechnung ist für allgemeine Fälle so kompliziert, dass sie mit vernünftigem Aufwand nicht zu stemmen ist. Für die Analyse des Gleichgewichts in einem Skiff ist gottseidank nur der zweite Term der gesamten Multipolentwicklung massgebend, das sogenannte Dipolmoment, es berechnet sich so:

Formel (3)
Damit lässt sich für die Massenverteilung eines Ruderers oder einer Ruderin in einem Skiff die relevante Näherung für das Gravitationspotential was Gleichgewicht angeht wie folgt approximieren:

Formel (4)
Nun lassen sich die zwei ersten relevanten Terme der Multipolentwicklung (4) der Massenverteilung ansehen und daraus lassen sich einfache Schlussfolgerungen ziehen.
Der erste Term auf der rechten Seite ist der sogenannte Monopolterm er beschreibt die ganze Masse des Systems, hier also die Summe der Masse aus Skiff und Ruderer/Ruderin, und das ist ein winkelunabhängiger Term der für das Gleichgewicht keine Rolle spielt denn das gesamte Gewicht aus Ruderer/in und Boot wird durch den Auftrieb auf dem Wasser im Gleichgewicht gehalten und hat keinen Einfluss auf Kippbewegungen. Der zweite Term, also der Dipolterm ist absolut entscheidend um die Probleme der Gleichgewichtslage zu erklären. Da ein/e Ruderer/in in einem Skiff von der relativen Massenverteilung die gesamte Systemmasse deutlich dominiert (etwa 5:1) ist das Dipolmoment im Wesentlichen durch die Massenverteilung im Körper der sitzenden Ruderperson konzentriert. Anschaulich lässt sich das so visualisieren:

Abbildung 1 Skiffruderer in leichter Schräglage
Der blaue Pfeil symbolisiert das Dipolmoment der Massenverteilung aus Ruderer und Skiff als komplexes System vieler Massenpunkte, es ist parallel verbunden mit der Rückgratlinie des Ruderers/Ruderin und zeigt in dieser Verlängerung nach oben, im Gleichgewicht exakt parallel zur z-Achse. Bei Schräglage der Ruderperson zeigt das Dipolmoment sofort in eine Richtung die zur z-Achse mit einem Winkel geneigt ist. Aufgrund der Dominanz der Masse des Ruderers bzw. der Ruderin folgt das Dipolmoment der gesamten Masseverteilung unmittelbar jeder Bewegung des Oberkörpers sofern der von der senkrechten Richtung abweicht. Hier spielt vor allem in sehr leichten Booten das grosse relative Massenverhältnis zu Gunsten des Ruderers (zu Lasten des leichten Skiffs) eine wichtige Rolle für die Stabilität während dem Rudern. Die Massenverteilung wird dominiert durch das Dipolmoment und die Gesamtmasse wird durch Auftrieb im Gleichgewicht gehalten und ändert sich nicht bei Kippbewegungen. Damit lässt sich für die bestmögliche Stabilität des Ruderers und der Ruderin im Skiff die einfache Forderung aufstellen:
In leichten Rennbooten wo die Masse der RuderInnen die gesamte Systemmasse dominiert ist es von äusserster Wichtigkeit während des Ruderns immer mit guter Körperspannung aufrecht im Boot zu sitzen, auch bei Wellengang. Kleine Schwankungen durch Wellen müssen immer mit den kleinen Korrekturbewegungen der Ruder ausgeglichen werden.
2 Kraftstoss als physikalisches Prinzip der Ruderbootsbewegung
Zuerst müssen wir verstehen weshalb wir ohne Motor ein Ruderboot auf dem See überhaupt vorwärts bewegen können. Es gilt das allgemeine Newtonsche Prinzip, dass ein massebehafteter Körper im Zustand der geradlinigen gleichförmigen Bewegung verharrt sofern er nicht äusseren Kräften ausgesetzt ist die seinen Bewegungszustand ändern können. Wenn wir für diese erste allgemeine Betrachtung die Reibung durch Wasser der Einfachheit halber vernachlässigen bedeutet dies, dass ein Ruderboot ohne Motor durch seine physikalischen Eigenschaften allein nur stehen bleiben oder mit konstanter Geschwindigkeit geradeaus fahren kann. Wie können die Ruderer und Ruderinnen die im Boot sitzen das Boot trotzdem von innen heraus beschleunigen?
2.1 Impulsübertrag vom Ruderblatt aufs Wasser während eines Ruderschlags
Gottseidank befinden wir uns mit dem Ruderboot nicht im Vakuum sondern auf dem schönen See und das Wasser ist unser bester Freund da es als Fluid mit relativ geringer Viskosität und trotzdem sehr hoher Massendichte ein ideales Medium ist um Kraft vom Boot auf die Umgebung zu übertragen. Für die Analyse der möglichen Beschleunigung des Ruderboots während eines kompletten Ruderschlags ist es in erster Betrachtung irrelevant auf welche Weise die Kraft auf die Ruderblätter übertragen wird. Die senkrecht ins Wasser gestellten Ruderblätter üben Druck aus auf das Wasser und schieben das Boot nach dem Prinzip actio=reactio mit einem Kraftstoss durch den Ruderer in die andere Richtung. Diese Kräfte sind wegen des Trägheitsprinzips im Gleichgewicht, die Kraft die aufs Wasser übertragen wird spürt das Boot exakt gleich gross mit umgekehrtem Vorzeichen, so dass die Summe der Impulse von Boot und bewegter Wassermasse null bleibt. Am Ende der Vortriebsphase hat der Ruderer durch seinen Kraftstoss dem Boot einen Impuls übertragen und es um diesen Betrag schneller gemacht. Das Trägheitsprinzip bedeutet, dass der exakt gleiche Impuls mit umgekehrtem Vorzeichen auf die Wassermassen des Sees übertragen wurde. Es ist nicht ganz klar wie stark das Wasser dabei überhaupt bewegt wird denn bei perfekt senkrecht stehenden Ruderblättern entsteht kaum Strömung und man kann sich sozusagen gegen eine sehr lange Schicht aus Wasser mit sehr hoher Masse abstossen. Der Impulsübertrag auf das Wasser hinter den Ruderblättern ist das Produkt aus bewegter Wassermasse mit geänderter Geschwindigkeit. Je perfekter der Ruderschlag ausgeführt wird umso länger ist die effektive Wassersäule an der die Ruderblätter sich abstossen können und diese Masse ist so gross, dass die resultierende Geschwindigkeit der bewegten Wassermasse gegen null geht. Es ist vergleichbar mit dem Rückstoss einer Billardkugel am Tischrand. Auch die Billardkugel überträgt einen Kraftstoss auf die Wand und ändert den Impuls so stark, dass sogar die Bewegungsrichtung der Kugel umkehrt. Dieser Impuls wird vom Billardtisch aufgenommen, der hat allerdings eine massiv höhere Masse als die Billardkugel, so dass die Geschwindigkeit die auf den Tisch übertragen wird vernachlässigbar klein ist. Wenn ein Ruderboot von oben beobachtet wird während der Vortriebsphase und man die absolute Position der Ruderblätter auf dem See beobachten könnte würde man feststellen, dass die Ruderblätter im absoluten Koordinatensystem nahezu am gleichen Ort bleiben, also kaum Wasser nach hinten verschieben. Deshalb spricht man im SRV[5] seit einiger Zeit auch nicht mehr von Durchzug sondern von Vortriebsphase oder Beschleunigung des Ruderboots, denn effektiv stösst der Ruderer oder die Ruderin das Boot an einer trägen sehr grossen Wassermasse ab die sich dabei kaum bewegt, wie der Billardtisch der vom Rückstoss der Kugel nichts mitbekommt. Das Ruder wird also nicht durch das Wasser gezogen, sondern stösst sich relativ dazu rückwärts ab. Wir sollten also das Bild im Kopf haben, dass wir uns während der Vortriebsphase wie an einer festen Wand abstossen, das kommt der Realität näher. Dies funktioniert nur deshalb so gut, weil Wasser eine sehr hohe Massendichte hat, bei geringerer Dichte würde die oberste Schicht leichter und schneller bewegt und der Vortrieb wäre wesentlich weniger effektiv.
Um einige allgemeine Schlussfolgerungen auf die optimale Schlaglänge zu ziehen kann man die allgemeine Formel für den gesamten Kraftstoss (=Impulsänderung) aufs Boot (inkl.Team) für einen vollständigen Ruderschlag wie folgt formulieren:

Formel (5)
Aufgrund der unterschiedlichen Hebel die während der Beschleunigung auf den Körper wirken, müssen beim Einsatz mit gestreckten Armen die Beine den Hauptanteil des Kraftstosses ausüben, denn unmittelbar nach dem Einsatz ist der Wasserwiderstand am grössten weil das Boot am Ende der Erholungsphase durch Reibung am meisten Geschwindigkeit einbüsst und deshalb die grösste Reaktionskraft erzeugt werden kann, die kann nur durch den Beinstoss effektiv erfolgen. Das Boot bewegt sich ja relativ zum Wasser und je schneller das passiert umso schwieriger ist es gleich grossen Druck auf die Ruderblätter auszuüben. Auch wenn das Wasser sich absolut kaum bewegt, so ist es aus Sicht des Ruderers/in genau umgekehrt: er/sie sieht das Wasser nach dem Einsatz und beginnendem Beinstoss immer schneller an sich vorbeiziehen, wer also zu spät einsetzt kann nicht mehr gleich viel Kraft aufbauen, weil das Wasser zu schnell das Ruderblatt mitnimmt. Bei zunehmender Geschwindigkeit und gegen Ende des Vortriebs können die Arme den Kraftstoss noch deutlich verlängern und bis zum optimalen Finish durchziehen.
Zur Abschätzung der grösstmöglichen Geschwindigkeitsänderung die bei jedem Ruderschlag aufs Boot übertragen werden kann müssen wir den Integranden auf der rechten Seite der Formel (5) ansehen. Da wir annehmen dass die Kraft im Integranden zu jedem Zeitpunkt des Ruderschlags nach oben begrenzt ist (bzw. ein zeitliches Kraftprofil ausübt das jeweils die gleiche Form hat) gibt es nur eine einzige Möglichkeit die Impulsänderung zu vergrössern und damit eine höhere Endgeschwindigkeit im Finish zu erreichen: man muss die Integrationsgrenzen erweitern, d.h. die Catchposition muss so früh und weit hinten wie möglich einsetzen und der Finish so spät wie möglich beendet werden, das führt zu einem grösseren Integral und damit grösserem Impulsübertrag nach dem Ruderschlag und grösserer Endgeschwindigkeit, bei genau gleichem Krafteinsatz. Ein schönes bebildertes Beispiel wie die Position der Ruderin an jedem Punkt des Ruderschlags aussehen soll ist z.B. vom Ruderclub Solothurn publiziert auf ihrer Webseite[6] In der Praxis gibt es allerdings Limitationen der Schlaglänge aufgrund der Biomechanik und der winkelabhängigen Krafteffizienz während der Beschleunigungsphase, die später publiziert werden.
3 Dynamik und Optimierung der Vorrollbewegung
Die vorhergehende Begründung der maximalen Schlaglänge um den grösstmöglichen Kraftstoss zu erzeugen gilt auch während des Ruderns mit konstanter Geschwindigkeit, hier kommt aber eine zusätzliche Komplikation hinzu aufgrund des notwendigen Vorrollens in der Erholungsphase nach dem Finish zum erneuten Einsatz. Das Prinzip actio=reactio gilt natürlich nicht nur für die Vortriebsphase wo der Kraftstoss gegen die Wassermassen auf das Boot übertragen wird, sondern noch viel empfindlicher auch in der Erholungsphase, wo der Ruderer zurück vom Finish in die Einsatzposition rollt und mit seiner Masse eine Impulsänderung in Fahrtrichtung aufs Boot überträgt. Die ganze Energie die der Ruderer oder die Ruderin mit grosser Mühe vorher in höhere Geschwindigkeit investiert hat in der Beschleunigungsphase wird anschliessend nur noch kleiner, als Kombination aus Impulsübertrag und daraus entstehender zusätzlicher Reibung, sowie der Reibung die auch ohne Vorrollen sowieso das Boot bremsen würde. Während die Regel einen möglichst langen Ruderschlag umzusetzen immer gilt, müssen wir für die Erholungsphase des Vorrollens sorgfältig beachten wie die Physik uns einen Streich spielt, wenn wir nicht aufpassen. Für die Berechnung der verschiedenen Effekte braucht es einige Notationen die wir später nicht mehr näher erklären, sie sind hier aufgelistet:

Tabelle 1 Symbole für physikalische Grössen
3.1 Impulserhaltung während Vorrollphase
Um wieder an den Einsatzpunkt zu kommen ist der Ruderer oder die Ruderin gezwungen zurück an die Einsatzposition zu rollen. Für jede Schlagzahl ist dazu ein optimal geeignetes Zeitfenster vorhanden das sehr eng definiert ist und deshalb wenig Spielraum lässt. Es zeigt sich, dass ein optimales Verhältnis zwischen Vortrieb und Ruhephase etwa 1:2 ist für einen effizienten Ruderschlag. Bei sehr hohen Renngeschwindigkeiten nähern sich diese Phasen etwas an, aber das ist ein Optimierungsprozess am physikalischen Limit auf den ich hier nicht eingehen werde. Wir dürfen damit annehmen dass bei gegebener Schlagzahl die Zeit für die Vorrollphase exakt vorgegeben ist. Nun haben wir verschiedene Möglichkeiten den Rollsitz zu bewegen und diese haben leider alle negative Effekte auf die Endgeschwindigkeit. Ohne ausüben von Kräften mit den Ruderblättern gilt für jede bewegte Masse im System Ruderer und Boot, dass die Summe aller Impulsänderungen immer verschwindet gemäss folgender Formel (die Vorzeichenkonvention ist positiv in Richtung der Fortbewegung des Ruderboots):

Formel (6)
Das bedeutet also, dass unabhängig von der Geschwindigkeit des Vorrollens immer ein zusätzlicher Impuls auf das Boot übertragen wird, was auf den ersten Blick ein Vorteil scheint, der sofort wieder verschwindet wenn man genauer betrachtet wie sich der Strömungswiderstand des Bootes verhält als Funktion der Geschwindigkeit.
3.2 Strömungswiderstand eines Bootes als Funktion der Geschwindigkeit
Bei typischen Rudergeschwindigkeiten und der strömungsoptimierten Geometrie eines Rennbootes erzielt man extrem hohe Reynoldszahlen der Strömung, was bedeutet dass sich die Grenzschicht des Wassers entlang des Bootsrumpfes klar im turbulenten Bereich befindet und die entsprechenden Formeln der Strömungswiderstände verwendet werden müssen die hier kurz aufgelistet werden ohne nähere Begründung.

Formel (7) Strömungskennzahl für schlanke Körper im Wasser

Formel (8) Reibungskraft auf Boot ohne Vorrollen im stationären Geschwindigkeitsbereich

Formel (9) Koeffizient für reale Reynoldszahl

Formel (10) Dragkoeffizient für Skiff

Formel (11) Massendichte Wasser

Formel (12) Effektiv benetzte Fläche für Drag-Schleppreibungskraft
Diese Formeln sind exakt und können die tatsächlich auftretenden Reibungskräfte und Geschwindigkeitsverluste gut erklären, nur ist die konkrete Berechnung ziemlich aufwändig für einen konkreten Fall einer Rollsitzbewegung, wir beschränken uns auf Schlussfolgerungen aufgrund der hier auftretenden Potenzgesetze der Strömungswiderstände. Nach realistischen Annahmen über die Rauhigkeit der Bootshülle befindet sich ein Ruderboot im hydraulisch glatten Limes und im Moody Diagramm[7] kann der Wert des Skalierungsexponenten der Reynoldszahl auf ca. -0.25 abgeschätzt werden. Damit skaliert der Strömungswiderstand am Ruderboot ungefähr mit 𝑣^1.75, also stark überlinear, nahezu quadratisch.
3.3 Rollsitzbewegung und Einfluss auf zusätzlichen Bootsimpulsverlust
Während der Erholungsphase üben die Ruder keine Kräfte aufs Boot aus, aber die Masse des Ruderers die um vieles grösser ist als ein leichtes Ruderboot übt grossen Einfluss auf den Impuls des Ruderboots aus das sich in entgegengesetzte Richtung (leicht vorwärts) schneller bewegt was in Videoaufnahmen von Ruderrennen gut sichtbar ist durch leichtes Wippen des Bugballs in Fahrtrichtung wenn das Team in die Einsatzposition vorrollt. Die allgemeine Reibungskraft welche am Boot nur aufgrund der Rollbewegung zusätzlich bremsend angreift als Funktion der Bootsgeschwindigkeit beim Finish und beliebig angesetztem Rollsitzgeschwindigkeitsprofil sieht so aus:

Formel (13)

Formel (14)

Formel (15)

Formel (16)

Formel (17)
Die knapp unterquadratisch rasch zunehmende Reibungskraft ist ein ernsthaftes Problem, wenn der ganze Geschwindigkeitsverlust durch Vorrollen minimal gehalten werden soll. Die exakte Berechnung des abnehmenden Geschwindigkeitsprofils des Bootes unter Berücksichtigung der Rollsitzgeschwindigkeit muss das Integral des Kraftstosses der zeitlich abhängigen Reibungskraft von der Bootsgeschwindigkeit abziehen, was den zweiten Term der Formel, die positive Zunahme des Impulses durch Vorrollen rasch vernichtet. Damit können wir das gesamte Bootsgeschwindigkeitsprofil (Formel (18) in der Ruhephase ausschliesslich als Funktion der Rollgeschwindigkeit ausdrücken wie folgt: (durch Elimination von "Delta v Roll / B (T)" mit (6) und durch einsetzen von (17) im Kraftstossintegral in (19) das den Reibungsverlust durch Rollsitzbewegung zu jedem Zeitpunkt t des Rollsitzgeschwindigkeitsprofils beschreibt)

Bootsgeschwindigkeitsprofil

Rollgeschwindigkeit

Delta v Roll / B (T)

Formel (18)

Formel (19)
Leider ist diese Formel zwar korrekt aber trotzdem etwas unhandlich da sie recht komplex meist nur numerisch auszuwerten ist für ein vorgegebenes Rollsitzgeschwindigkeitsprofil . Sie ist dafür allgemeingültig für beliebige Rollsitzgeschwindigkeiten, und deshalb können wir im folgenden nur die Konsequenzen diskutieren die für drei verschiedene typische Geschwindigkeits-Profile entstehen.
3.4 Optimale Vorrollphase

Gleichförmige Rollsitzbewegung

Geschwindigkeitsprofil gleichförmig
Hier ist der idealste Vorrollprozess gezeigt. Der Ruderer oder die Ruderin bewegt sich mit konstanter Geschwindigkeit vom Finish bis zur Einsatzposition im dazu zur Verfügung gestellten Zeitfenster das durch die Schlagzahl eng vordefiniert ist.
3.5 Zu schnelle Beschleunigung

Beschleunigte Rollsitzbewegung nach Finish

Beschleunigung bei Beginn Vorrollen
Ein typischer Anfängerfehler ist es, unmittelbar nach dem Finish hektisch bereits mit dem Vorrollen zu beginnen, was nicht nur den Rhythmus eines ganzen Bootes extrem stört, sondern vor allem sehr hohe Reibungskräfte schon zu Beginn dieser Phase provoziert. Wer zu schnell vorrollt muss am Ende wieder abbremsen um an die richtige Einsatzposition zu gelangen was die Synchronisierung mit den anderen im Boot erschwert und im Skiff eine unstabile Bootslage provoziert vor dem Einsatz der die heikelste Phase des ganzen Ruderschlagablaufs ist.
3.6 Zu später Start mit Beschleunigung am Ende
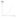
Zu spät einsetzende Rollsitzbewegung

Beschleunigter Rollsitz erst kurz vor dem Einsatz
Was absolut entscheidend ist die hier knapp unterquadratisch einsetzende Reibungskraft. Um zusätzliche Reibungsverluste durch zu hohe Rollgeschwindigkeit vollständig zu eliminieren dürfte man gar nicht vorrollen was offensichtlich keine Option ist. Jede Abweichung von der absolut gleichförmigen Vorrollbewegung bringt das Boot aber während eines wesentlichen Teils dieser Phase in den durch massiv höhere Reibung definierten roten Bereich und das bremst das Boot in beiden ungünstigen Fällen deutlich stärker ab. Die Fläche unter den Geschwindigkeitsprofilen muss in jedem Fall gleich gross sein da der Rollweg durch die Rollschiene und den Einsatzpunkt exakt vorgegeben ist und eingehalten werden muss.
4 Kraftübertragungseffizienz während des Vortriebs
Die Hebelgesetze am Ruder setzen das Drehmoment das vom Ruderer erzeugt wird gleich dem Drehmoment welches via Ruderblatt mit der parallelen Kraftkomponente auf das Wasser Druck ausübt (solange das Ruder nicht bricht und gleich elastisch auf beiden Seiten ist stimmt das)

Kraftkomponente
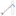
Abbildung 2 Kraftübertragungsgeometrie während Beschleunigungsphase

Formel (20)

Formel (21)
Anhand dieser Abbildung sieht man die konstruktionsbedingte Einschränkung der optimalen Erzeugung einer parallelen Kraftkomponente in Fortbewegungsrichtung. Sie wird maximal nur in der senkrechten Ruderstellung erreicht, beim Winkel a=0. Es ist offensichtlich unmöglich zu jedem Zeitpunkt die ganze Kraft ausschliesslich in Vortrieb umzusetzen deshalb ist die optimale Schlaglänge durch diese Ineffizienz sowie Biomechanik eingeschränkt. Die ideale Stemmbrettposition sollte so gewählt werden, dass sie mit der durch den Körper optimal möglichen maximalen Kraftübertragung übereinstimmt, was ungefähr am Ende des Beinstosses der Fall ist so dass die Stemmbrettposition als Faustregel so eingestellt werden kann, dass der Ruderer oder die Ruderin mit durchgestreckten Beinen und gestreckten Armen das Ruder exakt rechtwinklig zum Boot halten kann. Genauere Diskussionen sind von der Körpergeometrie abhängig und nicht Thema dieses Artikels.
5 Effizienz der Kraftübertragung auf die Ruderblätter
Ein unterschätztes Problem der Effizienz der Kraftübertragung während des Ruderschlags ist der korrekte Winkel mit dem das Ruderblatt durchs Wasser gezogen wird. Der Bootsbauer hilft uns natürlich sehr, indem die Dollen zwar abgerundet aber dennoch in zwei deutlich unterscheidbaren um 90 Grad versetzten Sollpositionen die Manschette des Ruders aufnehmen können, das Ruder ist zwar leicht drehbar in den Dollen aber es rastet senkrecht in der Vortriebsposition und waagrecht in der Erholungsphase sehr gut definiert in zwei zueinander senkrecht stehenden Winkeln in die optimale Position ein. Nun gibt es aber aufgrund mangelnder Disziplin während des Ruderns durchaus Probleme in der Kraftübertragungseffizienz die vor allem durch die folgenden zwei Fehler in der Ruderblattposition entstehen.
5.1 Eintauchtiefe des Ruderblatts
Es ist extrem wichtig, dass während des ganzen Vortriebs die Ruderblätter vollständig im Wasser eingetaucht bleiben, damit die Kraft die der Ruderer/die Ruderin auf das Blatt ausübt auch vollständig auf das Wasser übertragen wird. Ansonsten kann bei exakt gleicher Kraftausübung nur deutlich weniger Wasserdruck für den Kraftstoss erzeugt werden was umgehend geringeren Impulsübertrag und deshalb reduzierte Geschwindigkeit zur Folge hat. Der maximale Wasserdruck der entsteht durch die Kraft auf das vollständig eingetauchte Ruderblatt ist einfach zu berechnen:

Wasserdruck

Kraft

Formel (22)
Bei unvollständig eingetauchten Blättern, was bei Wellengang nahezu unvermeidlich, aber bei ruhigem Wasser eine Frage der Konzentration und Disziplin ist, reduziert sich der Wasserdruck rasch deutlich wenn das Blatt nicht vollständig im Wasser liegt. Die Kraft auf dem Ruderblatt übt nur Druck auf das Wasser aus mit der vollständig benetzten Fläche, der Druck gemäss Formel (22) reduziert sich dementsprechend bei nur teilweise eingetauchten Ruderblättern.
5.2 Eintauchwinkel des Ruderblatts in Catchposition (Einsatz)
Noch heikler und weniger offensichtlich was Verlust and Kraftübertragungseffizienz betrifft ist der korrekte Blattwinkel beim Eintauchen in der Catchposition (beim Einsatz) Die Blätter sollten vollständig geöffnet und direkt senkrecht an der hintersten Position ins Wasser eingetaucht werden wo der maximale Druck auf die Blätter aufgebaut werden kann. Wenn die Blätter unvollständig aufgedreht eingetaucht werden reduziert sich der Wasserdruck ebenfalls mit dem Cosinus beta des Blattwinkels, da nur die in Fahrtrichtung effektiv sichtbare Fläche des Ruderblattes den Druck aufs Wasser aufbauen kann. Die Kombination dieser zwei beschriebenen Fehler im Ruderblattwinkel kommt leider in der Ruderpraxis ziemlich häufig vor und sie hat durchaus bemerkenswerten Effekt auf die insgesamt ans Wasser übertragbaren Kraftstösse.
5.3 Geometrische Darstellung eines unsauber geführten Ruderblattes

Abbildung 3 Geometrie eines falsch geführten Ruderblattes im Vortrieb
In dieser Grafik sind beide Fehler gleichzeitig eingezeichnet. Obwohl sie auf den ersten Blick ziemlich harmlos aussehen, haben sie deutliche Effekte auf die übertragbaren Impulse während der Beschleunigungsphase (Vortrieb). Unvollständig eingetauchte Blätter reduzieren den Impulsübertrag direkt proportional zur mit Wasser benetzten Blattfläche, falsch eingestellte Winkel proportional zum Cosinus des Blattwinkels beta, was für kleinere Abweichungen quadratische Effekte erzeugt und somit eher vernachlässigbar ist. Trotzdem soll hier ein durchaus praxisnahes Beispiel berechnet werden um wie viel sich der Wasserdruck reduziert wen bei der Catchposition sowohl Blattwinkel als auch Eintauchtiefe inkorrekt sind:

Formel (23a)

Formel (23b)
Im hier berechneten durchaus typischen Beispiel eines unsauberen Einsatzes reduziert sich der Druck aufs Wasser bereit auf 60% des maximal möglichen Druckes, wohlgemerkt bei exakt gleichem Kraftaufbau des Ruderers/der Ruderin, die beide das Gefühl haben optimal Rudereinsatz zu geben, sie merken keinen Unterschied in der ausgeübten Kraft (das Boot leider schon) Auch wenn in der zweiten Hälfte des Vortriebs die Ruderblätter sauber aufgedreht und vollständig mit Wasser benetzt werden ist für die ganze Beschleunigungsphase der gesamte Impulsübertrag mit diesem Einsatzfehler auf unter 80% zusammengefallen, was in einem Rennen katastrophale Konsequenzen hätte wenn es zu oft vorkommt. Noch viel hässlicher als der Verlust der Kraftübertragung ist die zusätzlich auftretende Dragkraft nach unten. Sie entsteht, weil die Reaktionskraft auf das Ruder durch den Wasserwiderstand immer senkrecht auf dem Ruderblatt angreifen muss. Wasser ist nahezu reibungsfrei und fliesst seitwärts entlang des Ruderblattes weg sofern es nicht ganz senkrecht steht, nur dann steht das Wasser direkt am Ruderblatt ganz still und überträgt die Kraft statisch auf das Ruderboot. Die immer senkrecht wirkende Reaktionskraft "F_push,react,norm" auf das Ruderblatt hat eine Komponente senkrecht nach unten die hier mit "F_drag" bezeichnet wird. Ein falsch nicht voll aufgedrehtes Ruderblatt mit beta ungleich 0 wird also unmittelbar nach Einsetzen des Beinstosses mit "F_drag" nach unten gezogen, das kann so dramatisch schnell gehen bei grosser Kraft dass man das Blatt nur mit Mühe zurück an die Wasseroberfläche bringt und wenn der Winkel nicht sofort senkrecht gestellt wird riskiert man bald einen Krebs am Ende des Vortriebs und einen Skiff rasch zum Kentern.
6 Synchronisierung der Kraftstösse in einem grösseren Ruderteam
Ich gehe in diesem Artikel nicht näher darauf ein was passiert in einem grösseren Boot mit 4-8 RuderInnen wo die Anforderungen an die Synchronisierung massiv höher sind und deshalb grosse Disziplin notwendig ist um gute Bootsgeschwindigkeit zu erreichen. Ganz allgemein lässt sich folgendes sagen was passiert wenn einzelne Teammitglieder zum Beispiel zu spät zum Einsatz kommen oder deutlich kürzere Vortriebswege vorziehen:
- Zu spät einsetzen bedeutet, dass die maximale Kraft des Beinstosses der durch den Schlagmann vorgegeben wird nicht mehr erreicht werden kann und so der Beitrag zum Vorschub massiv verkleinert wird
- Zu kurzer Ruderschlag bedeutet gemäss erster Bemerkung zum Kraftstoss klar ungenügenden Impulsübertrag durch verschenken von möglichem Vortriebsweg, das gilt auch unabhängig von Synchronisation, es ist auch bei guter Synchronisierung ein Problem.
Die Synchronisierung im Team ist ein komplexes Thema das nicht näher erläutert werden soll, es ist aber offensichtlich dass nicht nur alle anderen im Boot gestört werden wenn der Rhythmus nicht stimmt, es führt rasch zu dramatischen Verlusten im Beitrag zur Impulsübertragung. Ein effizient auf optimaler Geschwindigkeit ruderndes Boot erfordert ein perfekt harmonisierendes im synchronen Rhythmus ruderndes Team.
7 Schlussfolgerungen für die Ruderpraxis
Dieser Artikel beleuchtet die physikalischen Hintergründe des Rudersports, erklärt aber nur im Detail was in der Ruderpraxis mit exakt gleichen Empfehlungen ebenfalls trainiert wird. Hier noch einmal die wichtigsten Aspekte des Ruderns die beachtet werden müssen:
- Immer aufrechte Haltung im Boot mit guter Körperspannung, Schwankungen durch Ruder korrigieren
- Möglichst langen Ruderschlag wählen, um maximalen Kraftstoss aufbauen zu können
- Ruderblätter beim Einsatz exakt senkrecht stellen und während ganzer Beschleunigungsphase sauber senkrecht führen, die Blätter müssen immer vollständig mit Wasser benetzt sein aber dürfen nicht abtauchen.
- Die ganze Vorrollphase soll mit exakt gleichmässiger Geschwindigkeit durchgeführt werden, im Idealfall etwa doppelt so viel Zeit wie für den Vortrieb budgetieren, abhängig von Schlagzahl
- Im Team hohe Disziplin auf saubere Synchronisation legen inkl. gleicher Schlaglänge für alle
8 Danksagungen
Ich möchte mich an dieser Stelle herzlich bedanken bei meinem Physik-Studienfreund von der ETHZ Prof.Dr. Daniel Weiss, [https://www.fhnw.ch/de/personen/daniel-weiss] Dozent für Thermo- und Fluiddynamik an der FHNW Brugg-Windisch, ein ausgewiesener Experte in Fluiddynamik, der mir wertvolle Hinweise gegeben hat in der korrekten Beschreibung von inkompressiblen turbulenten Strömungen im hydraulisch glatten Limes und den stark nicht linearen Reibungskräften die dabei auftreten. Ohne seine Hinweise wäre das wichtige Kapitel zur Vorrollbewegung hier wohl nicht geschrieben oder nur mit einem latenten Unwohlsein abgehandelt worden. Sarah und Bruno möchte ich danken für einige wertvolle Hinweise zu aktuell verwendeter Terminologie im SRV und Gewichtung einiger Abschnitte hinsichtlich der Bedeutung für das Erlernen des Rudersports
Zug, Matthias Krieger, SCZ, 30.8.24
[1] «Rowing Performance Analysis Using Motion Sensors», Franz Gravenhorst, Diss. ETHZ No. 22478, 2015; https://www.research-collection.ethz.ch/handle/20.500.11850/155046
[2] «Die Physik des Rudersports unter biomechanischen Gesichtspunkten», Sascha Adrian, Immanuel-Kant Schule Rüsselsheim, Abiturfacharbeit Sport&Physik, 2004; http://www.swadi.de/facharbeit/pdf/Physik_des_Rudersports.pdf
[3] «Biomechanische Grundlagen sportlicher Bewegungen», Ditmar Wick, Lehrbuch der Biomechanik, Spitta Verlag GmbH, Balingen, 2005; www.spitta.de
[4] https://www.staempfli-boats.ch/skiff-st1/
[5] Private Bemerkung von Coach Sarah Zurbrügg-Greenaway, See Club Zug
[6] https://solothurner-ruderclub.ch/verein/ruderwissen/rudertechnik/
[7] «Fluidmechanik, SG Maschinenbau» Prof.Dr.D.Weiss FHNW, Kap. 8 Inkompressible Aussenströmungen, 2023









